thomasabishop/eolas
1
0
Fork 0
Code Issues Pull requests Projects Releases Packages Wiki Activity Actions
eolas/neuron/666a9949-2ad4-4228-a102-35f508a9db5d/Creating_memory_with_NAND.md
thomasabishop 849653ceb0 Autosave: 2025-02-11 18:11:49
2025-02-11 18:11:49 +00:00

3.1 KiB
Raw Blame History

tags
logic-gates
binary
memory

Creating memory with NAND gates

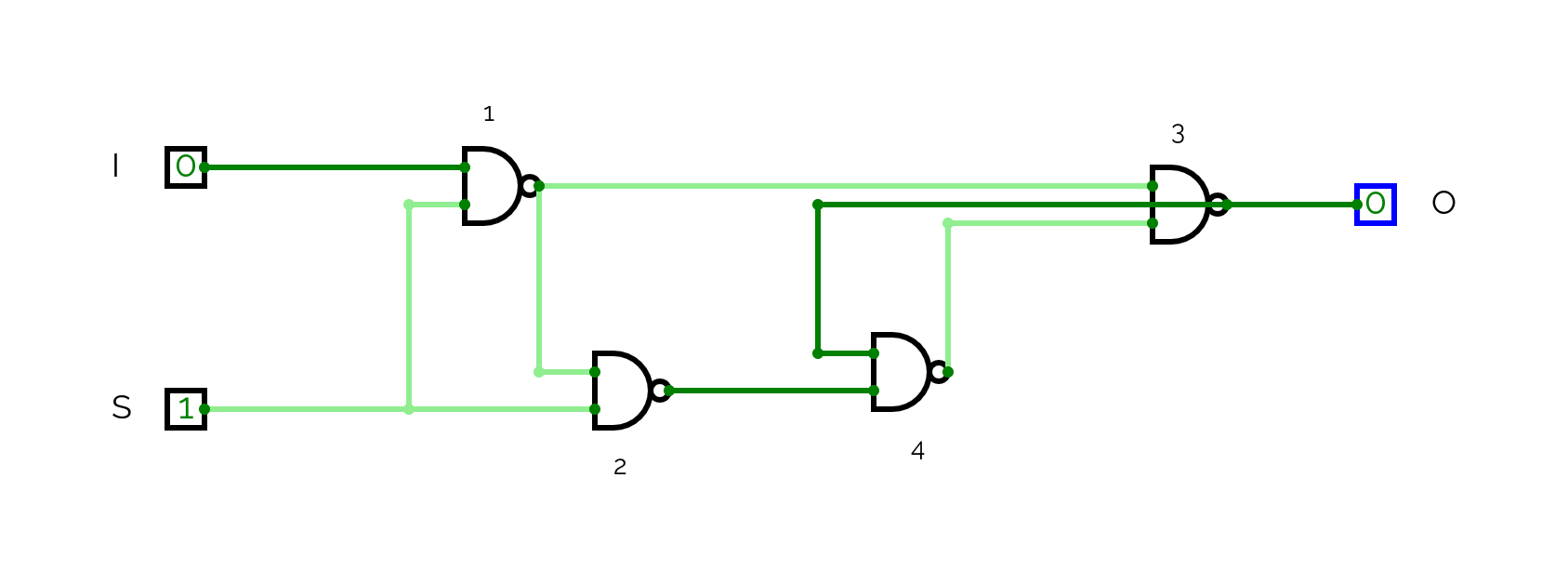
The logic circuit below demonstrates how memory can be created using NAND gates. A single bit is stored in memory.

Interactive version of circuit:

Components

  • I is where we input the bit that we want to remember.
  • O is the output of the remembered bit
  • S is an input that tells these gates when to set the memory.
  • A, B, C are internal wires that represent the individual bit values which channel into each gate

State changes

First state: S ON, I OFF

  • Start with S ON and I OFF.
  • Given the logic of NAND, A will be on.
  • This means Gate 2 is receiving ON from A and ON from S therefore B is OFF
  • Moving to Gate 4 it is receiving OFF from B and it's other input is not activated so is therefore also OFF. Consequently C is ON
  • C is fed as the second input into Gate 3, thus we have both inputs (A and C) as ON, therefore the output will make O OFF

Upshot: With S ON, output is the same as input

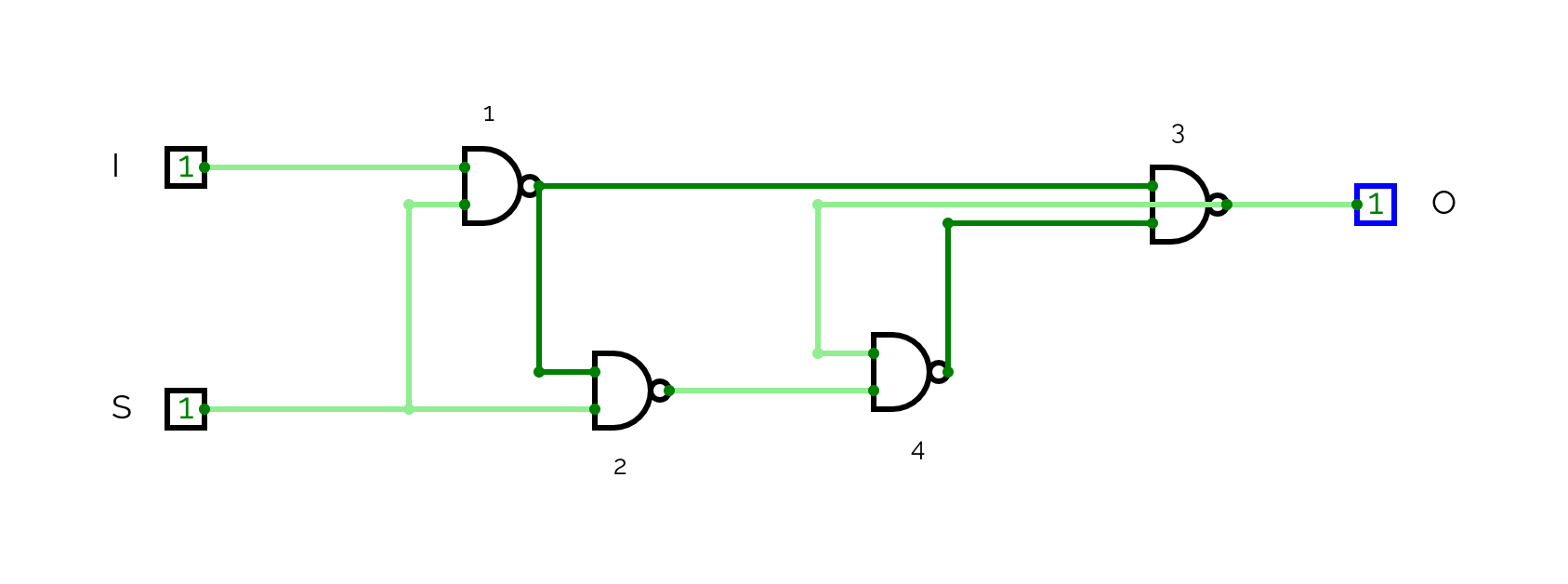
Second state: both S and I ON

  • With S and I both on, Gate A will be OFF
  • Gate 2 is receiving OFF from A and ON from S therefore B is ON
  • A feeds into Gate 2 which is receiving ON from S, therefore the output (B) will be ON
  • A feeds into Gate 3 and the other input is OFF, therefore Gate 3 is outputting ON. Thus O is ON
  • O feeds back to Gate 4 which is receiving ON from B thus we have two ON inputs going into Gate 4, turning C off
  • This means the two inputs going into Gate 3 are both OFF, keeping O ON

Upshot: With S on, the output is again the same as the input

So far we have seen that when S is ON you can change I on and off and O will change with it.

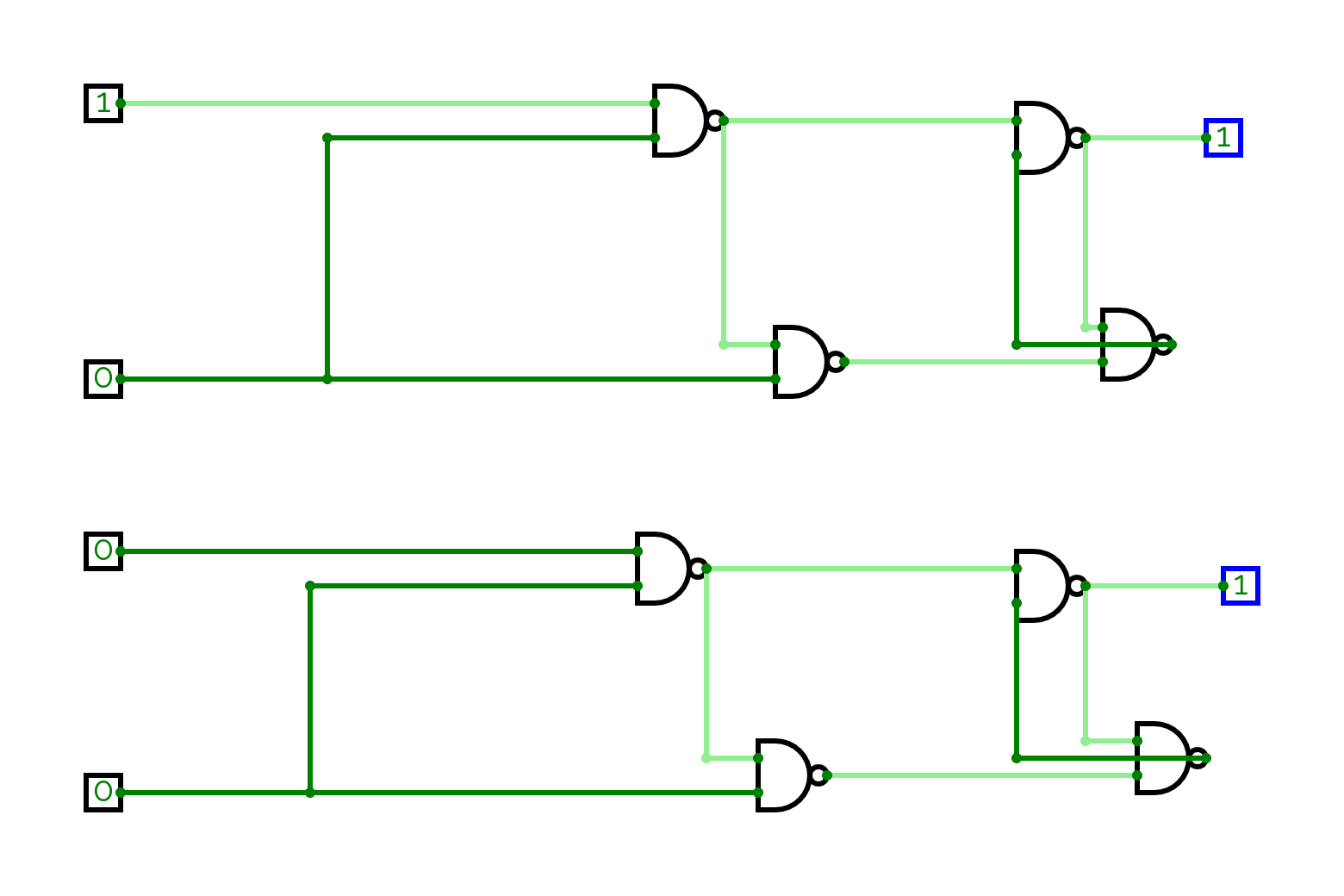
Memory

When S is ON, O will mirror whatever state I is in. However if you turn S OFF, O will remain in whatever state it was when S was turned OFF. You can toggle I as much as you like, O will remain in its previous state. Hence creating a memory store of the past value of I.

The specific reason for this is that, if S is OFF, both A and B are ON since at Gate 1: ON (I) + OFF (S) = ON and OFF (I) + OFF (S) = OFF and at Gate 2: OFF (Gate 1) + OFF (S) = OFF

This is illustrated in the diagram below. The space occupied by A and B remains on (note it is illuminated) regardless of the state of I.